Polymial Notes

Veröffentlicht am | Edited on

本文致力于介绍多项式家族的算法以及一些有趣的数学知识。另外我打算把所有数学学习内容都放到这个Post，包括组合数学，容斥与莫比乌斯反演等
img
可以学习如何书写

Mobius function and inversion

感觉这是个在数论上挺有用的东西，所以来学习一下（本来想着NOIP前不学新算法。。。）

==定義==
假設對於數論函數 $f(n)$ 和 $F(n)$，有以下關係式：

$F(n) = \sum_{d|n} f(d)$

則將其默比乌斯反轉公式定義為：

$f(n) = \sum_{d|n} \mu (d) F \left( \frac{n}{d} \right)$

== 一般形式 ==
設$F(x)$及$G(x)$為定義在$[1, \infty)$上的複值函數並且

$ G(x)=\sum_{1\leqslant n\leqslant x}F\left( \frac{x}{n}\right) $

則

$ F(x)=\sum_{1\leqslant n\leqslant x}\mu(n)G\left( \frac{x}{n}\right) $

== 证明 ==
设$\sum{d\mid n}\mu(d) = [n = 1]$，又由于$f(n) = \sum{d\mid n}[\frac{n}{d} = 1]f(d)$，代入得到$f(n) = \sum{d\mid n}\sum{m\mid \frac{n}{d}}\mu(m)f(d)$。

由于$\sum{d\mid n}\sum{m\mid \frac{n}{d}}$的限制条件其实就是$md\mid n$，故等式可以写成：$f(n) = \sum{m\mid n}\mu(m)\sum{d\mid \frac{n}{m}}f(d) = \sum_{m\mid n}\mu(m)F(\frac{n}{m})$。

狄利克雷卷积对于数论函数的定义是：

假如两个数论函数f(n),g(n)

因此很容易证明狄利克雷卷积满足交换律。

也可以证明狄利克雷卷积满足结合律 ， 只需要证明左右同时作用在n上时相等即可。

然后这就说明了数论函数在卷积意义下构成了交换群。

这时我们需要了解狄利克雷卷积的单位元函数，所谓单位元函数在群论中已经有所见识，很容易想到狄利克雷卷积的单位元函数r满足

从上面定义式来看显然

我们来证明一个引理

n = 1 时显然成立

n > 1时

将n写成质因数唯一分解形式

于是

img

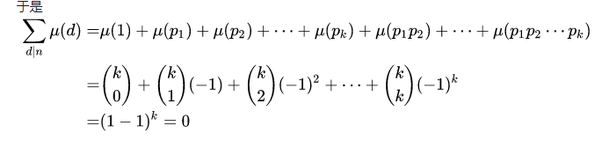
现在我们来观察如下三个函数：

我们很容易发现

因为

容斥原理

看一道经典的容斥的题目.

有n个人,第$i$个人不能站在第$i$个位置上,问方案数. $n\leq 1e5$

事实上高中数学必修一集合一章有n=3的题目。。。我们画venn图可以得到答案是2。

对于1e5，我们很容易想到推广的容斥公式

还是用集合来考虑，对于全集是n的全排列，一个人站对就是所有集合，2人站对就是两个集合的交集部分，三个人就是3个集合的交集部分，这样一来计算全集除去n个集合的面积就是答案，即为上面的公式。

看上去这道题解决了，那么我们也许还有其他思路来做这道题。

设f(n)表示n个人随便站的方案数，g(n)表示n人都站错的方案数,那么

似乎可以用上面介绍的反演，然而并不行，反演是针对除数函数的。。

所以我们用常用的脱裤子放屁法来将式子逆优化一下。

我们成功将$O(g(n))$的式子变成$O(ng(n))$。。

然后开始变魔术

由杨辉三角的对称我们可以得到

所以将$n-i=0$替换下,也就是将下面的n替换成n-i带入就是一样的QVQ。

式子有点复杂：

这里我们考虑$C{n-i}^{j}C{n}^{i}$的意义：从$n$中选两个大小为$i$和$j$的不交集合的方案数。

所以

其实对比左右发现这也是对称的，即左边的$i$和右边的$j$取得的值仅仅是顺序不用。

所以

改变求和顺序（不是无穷级数当然可以随便改啦，就跟提公因式一样，反正总枚举量一样）

其实条件相当于k+m<=n，只不过这样写最后才能完成二项式反演的形式

所以最后那个和式是什么？$f(n-i)$

显然

,因此我们就通过一句废话加上变魔术完成了对一个容斥公式的证明。

又由对称性，我们把它变得漂亮一点

至此，二项式反演就完成了

FFT Study Note

FFT学习笔记

Preface

Many things are from Flower_pks..Thanks very much.(Although I modify some contents that seems not to be right….)

复数

这个东西的基本运算和普通实数没什么区别,只不过带着$i$而已.

加减分开加,乘法就是交叉相乘,除法没研究过应该用不到，好像只需要乘到分子上就行了吧。

卷积 Convolution

卷积(Convolution)，准确来说是一种通过两个函数$f$ 和$g$ 生成第三个函数的一种数学算子.
而广义上其定义为：
$h(x)=∫_{-\infty}^{\infty}g(τ)⋅f(x−τ)dτ$

而此处我们讨论的是整次多项式域，那么就把其定义划归进多项式，得到

$A(x)B(x) = \sum\limits{i=0}^{n}\sum\limits{j=0}^{i}AjB{i-j}$

$A$与$B$都是$n-1$次多项式.

比较显然的是，在我们合并同类项的情况下，最终卷出来的结果应该有$2n+1$项。

点值表示法 DotMethod

上述多项式的形式成为系数表示法,我们可以由相异的$n+1$个点确定一个$n$次的多项式.

$f(x) ⇒ (x_1,y_1) , (x_2,y_2) …… (x_n,y_n)$

点值相乘 Dot Multiply

对于两个$n$次多项式,我们需要取$2n+1$个点.
$A(x) ⇒ (x1,y_1) , (x_2,y_2) …… (x{2n+1},y{2n+1}’)$
$B(x) ⇒ (x_1,y_1’) , (x_2,y_2’) …… (x{2n+1},y_{2n+1}’)$

由于我们取相同的$x$,所以只需要把$y$相乘.

$C(x) ⇒ (x1,y_1y_1’) …. (x{2n+1},y{2n+1}y{2n+1}’)$

这一过程是$O(n)$的.

不过很显然多项式求值是$O(n)$的,因此DFT(离散傅里叶变换)和IDFT(离散傅里叶逆变换)都是$O(n^2)$的.

接下来我们把它们优化到$O(nlogn)$

单位根 Unit Root

(这部分会有一些拓展和更新)

$\omega^n =1$

在一个复平面单位圆上以$\frac{2\pi}{n}$为幅角的$n$个根就是单位根.

欧拉公式:

$e^{ix}=cosx+isinx$
$x=2\pi$
$e^{2\pi i}=1=\omega^n$
$\omega=e^{\frac{2\pi i}{n}}$

这个根记作$\omega_n$,称为主次单位根.

对于其他主次单位根的$k$次幂,记为$\omega_{n}^{k}$

消去引理Elimination Lemma

$\omega{dn}^{dk} = \omega{n}^{k}$

proof: 可由欧拉公式得到:

$\omega{dn}^{dk} = e^{\frac{2\pi i dk}{dn}} = e^{\frac{2\pi ik}{n}} = \omega{n}^{k}$

折半引理Binary Lemma

对于任何大于0的偶数$n$，都有$n$个$n$次单位复根的平方的集合，等于$\frac{n}{2}个\frac{n}{2}$次单位复根的集合.

$(\omega{n}^{k})^2 = \omega{n}^{2k} = \omega_{\frac{n}{2}}^{k}$

$(\omega{n}^{k+\frac{n}{2}})^2 = \omega{n}^{2k+n}=\omega{n}^{2k}\omega{n}^{n}=\omega{n}^{2k}=\omega{\frac{n}{2}}^{k}$

单位根个数折半.(其实这就是共轭复数的平凡性质吧….)

那么接下来，如果对所有的$n$次单位跟平方一下，我们会发现$n/2$次单位根每个都恰好出现了两次——也就是说，在$n$个$n$次单位复数根平方的集合（朴素的集合，即不可重集）里，只有$n/2$个元素。我们参考上面那张图，它的意义就在于方向相对的两只向量，其平方相等。

那么把所有$n$单位根的平方画到一个数列上就是这样。

img

后面我们会通过对当前多项式构造两个多项式,使得他们关于$x^2$和当前多项式有关,然后就可以不断分治.

求和引理

$∀k ∤ n , \sum\limits{i=0}^{n-1}(\omega{n}^{k})^i = 0$

proof:

$\sum\limits{i=0}^{n-1}(\omega{n}^{k})^i$

$=\frac{(\omega{n}^{k})^n-1}{\omega{n}^{k}-1}$

$=0$

(分母不会为0,因为保证了$k ∤ n$)

当$k∣n$时,$\sum\limits{i=0}^{n-1}(\omega{n}^{k})^i = n$

离散傅里叶变换DFT

对于$n$次多项式$A(x) = \sum\limits_{i=0}^{n}a_ix^i$(这里我们假设最高次幂是$n-1$,不然单位根下标是$n+1$)

我们取$\omega{n}^{0}$~$\omega{n}^{n-1}$

多项式项数(注意是最高次幂+1)不是2的次幂就补足0,为了成功分治,只不过多了2倍常数

对于系数向量$\vec A = [a0,a_1…a{n-1}]$, 对于$k = 0,1,2,3….n-1$

定义$yk = A(\omega{n}^{k}) = \sum\limits{i=0}^{n-1}a_i\omega{n}^{ki}$

则称向量$\vec y = [y0,y_1….y{n-1}]$是向量$\vec A$的DFT.

FFT优化DFT

主要运用折半引理

对于$A(x)=\sum\limits_{i=0}^{n-1}a_ix_i$

构造

$A0(x) = a_0+a_2x^1+a_4x^2….+a{n-2}x^{n/2-1}$
$A1(x) = a_1+a_3x+a_5x^2……+a{n-1}x^{\frac{n}{2}-1}$

之所以这么构造是因为

$A(x) = A_0(x^2)+xA_1(x^2)$

也就是说

$A(\omega{n}^{k}) = A_0(\omega{n}^{2k})+A1(\omega{n}^{2k}) = A0(\omega{\frac{n}{2}}^{k})+A1(\omega{\frac{n}{2}}^{k})$

(注意$n$是2的次幂,无边界问题)

所以我们求单位根在多项式的值只需要求这两个多项式.

由于平方可以根据折半引理直接分治求出一半.

对于另一半

$A(\omega{n}^{k+\frac{n}{2}}) = A_0(\omega_n^{2k+n})+\omega_n^{k+\frac{n}{2}}A_1(\omega{n}^{2k+n}) = A0(\omega_n^{2k})+\omega_n^{k+\frac{n}{2}}A_1(\omega{n}^{2k}) $

最后一步化简是因为$\omega_{n}^{n} =1$

在复平面里单位圆依然有一些和实数平面相同的性质(非常平凡的)

$\omega{n}^{k+\frac{n}{2}} = -\omega{n}^{k}$

所以上面的表达式为

$A0(\omega_n^{2k})-\omega{n}^{k}A1(\omega{n}^{2k})$

这个是可以直接计算的.

来自Flower_pks的伪代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

int Lim = 1, N, M ;
function FFT(int lenth, complex *A, int flag){
	IF (Lim == 1) return ;
	complex A0[lenth >> 1], A1[lenth >> 1] ;//分成两部分
	for(int j : 0 to lenth by_grow 2) A0[j >> 1] = A[j], A1[j >> 1] = A[j + 1] ;
	FFT(lenth >> 1, A0, flag) ;
	FFT(lenth >> 1, A1, flag) ;
	complex Wn = unit(,) , w = (1, 0) ;//Wn是单位根，w用来枚举幂，即我们令主次单位根不变，由于其余单位根都是其整次幂，所以可以用一个w来记录到第几次幂
        /*此处求单位根的时候会用到我们的参数flag……嗯没错就用这一次，并且flag的值域为(-1, 1)……是的，只会有两个值*/
	for(int i : 0 to (length >> 1) by_grow 1 with w = w * Wn){//length拼错了.....
		A[i] = A0[i] + A1[i] * w ;//应用公式，下同 
		A[i + (length >> 1)] = A0[i] - A1[i] * w ; //顺便求出另一半，由折半引理可显然。 
	} 
} 
function Main{
	input(N), input(M) ;
	for(i : 0 to N by_grow 1) => input(A) ;
	for(i : 0 to M by_grow 1) => input(B) ; 
	while(Lim < N + M) Lim <<= 1 ;//Lim为结果多项式的长度（暂时），化为2的幂的便于分治（二分）
	FFT(Lim, A, 1) ;//两遍FFT表示从系数化为点值 
	FFT(Lim, B, 1) ;
	for(i : 0 to Lim by_grow 2) => A[i] *= B[i] ;//点乘法，此处需要重定义乘号，因为每一项现在表示的是一个点，有x和y两个属性qwq 
}

明确那个结构体数组每个元素$Ak$表示的就是$A(\omega{n}^{k})$

FFT优化IDFT

好像比上面更麻烦一点了.

先介绍一下范德蒙特矩阵:范德蒙矩阵是一个各列呈现出几何级数关系的矩阵.

显然有以下关系:

看样子我们可以矩阵求逆(其实我根本不会)

$O(n^3)$没有卵用.插值$O(n^2)$也不大行.

然后有这么一个推论:

$\forall j,k = 0,1,2…n-1 , V{n}’(j,k) = \frac{\omega{n}^{-jk}}{n}$

proof:

没记错的话矩阵求逆是可以被证明唯一的.

这意味着充分即必要.

我们只需要证明$VV’=U$

$U$是单位矩阵,对角线都是1.

对于相乘后的矩阵的元素$(i,j)$,其表达式为:

$\sum\limits{k=0}^{n-1}\frac{\omega{n}^{-ik}}{n}\omega{n}^{kj} = \frac{1}{n}\sum\limits{k=0}^{n-1}\omega_{n}^{k(j-i)}$

求和引理可知.当且仅当$j=i$的时候为1.

因此命题成立.

我们最后看一下DFT和IDFT

$DFT(\omega{n}^{k}) = \sum\limits{i=0}^{n-1}ai\omega{n}^{ik}$

$IDFT(yk)=\frac{1}{n}\sum\limits{i=0}^{n-1}yi\omega{n}^{-ik}$

所以最后IDFT出来的还要除$n$。

FFT的核心算法已经结束了。

放一下Flower_pks的伪代码吧，听清楚（虽然变量名有写错的）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

void FFT(int Lim,complex *A,int flag){
    if(Lim == 1) return ;
    complex A0[Lim >> 1], A1[Lim >> 1] ;
    for(int i = 0; i <= Lim ; i += 2)
        A0[i >> 1] = A[i], A1[i >> 1] = A[i+1] ;
    FFT(Lim >> 1, A0, flag) ;
    FFT(Lim >> 1, A1, flag) ;
    complex unit = (complex){cos(2.0 * Pi / Lim) , flag * sin(2.0 * Pi / Lim)}, w = complex(1, 0) ;//欧拉公式 
    for(int i = 0;i < (Lim >> 1) ; i ++, w = w * unit) {
        A[i] = A0[i] + w * A1[i] ;
        A[i + (Lim>>1)] = A0[i] - w*A1[i];
	}
}

int main(){
......................
FFT(A, 1), FFT(B, 1) ;
for(i = 0; i <= Lim; i ++) A[i] = A[i] * B[i] ;
FFT(A, -1) ;
......................
}

蝴蝶定理与蝴蝶操作 Butterfly Theorem and operation

如图

img

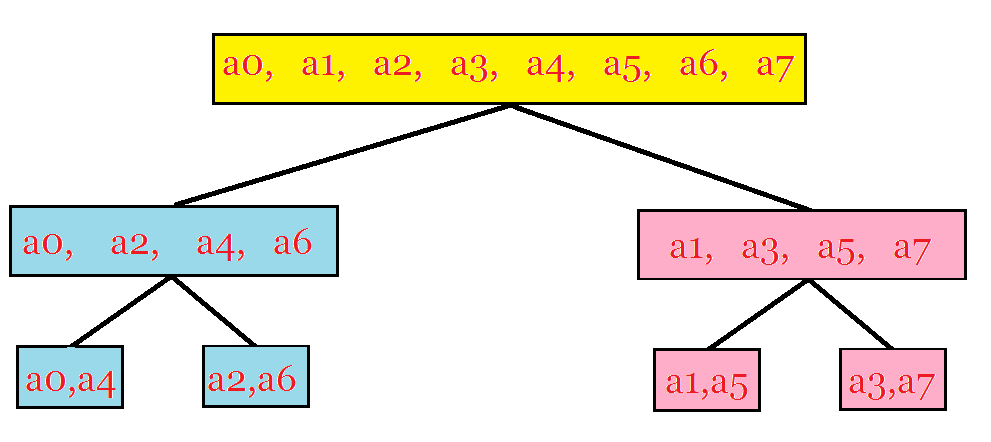
我们可以自底向上进行计算，常数会小很多。

  1. 成对地取出儿子节点，用蝴蝶操作计算出其DFT。
  2. 用这一步的DFT替换之前的；
  3. 直到我们迭代到根节点为止，否则返回step1

我们得把序列按照叶节点的顺序从左往右排好。

这个顺序可以打表发现。

比如原来是001现在是100

1
for(i = 0; i < Lim; i ++ ) R[i] = (R[i >> 1] >> 1) | ((i & 1) << (L - 1)) ;

真去研究怎么证明没有什么意义。

我们发现只要我们用迭代的过程模拟出回溯的过程即可。那么思路便有了：三层$for$，先枚举区间长度（1，2，4，8……），第二层枚举区间的起点，第三层遍历区间.

这次就真的结束了。

Code

递归版

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
#include <cstdio>
#include <cstdlib>
#include <algorithm>
#include <iostream>
#include <cmath>
#define maxn 2000005
int n , m , lim;

const double pi = acos(-1.0);
struct Complex
{
	double x,y;
	Complex operator + (const Complex p)const{
		return (Complex){x+p.x,y+p.y};
	}
	Complex operator - (const Complex p)const{
		return (Complex){x - p.x , y - p.y};
	}
	Complex operator * (const Complex p)const{
		return (Complex){x*p.x-y*p.y , y*p.x+x*p.y};
	}
}A[maxn] , B[maxn];

void FFT(int ln , Complex* T , int op)
{
	if(ln == 1) return ;
	Complex F[ln >> 1] , G[ln >> 1];
	for(int i = 0 ; i <= ln ; i += 2)
		F[i >> 1] = T[i] , G[i >> 1] = T[i+1];
	FFT(ln >> 1 , F , op);
	FFT(ln >> 1 , G , op);
	Complex Wn = (Complex){cos(2.0*pi/ln),sin(2.0*pi/ln)*op} , w = (Complex){1,0};
	for(int i = 0 ; i < ln >> 1 ; ++i , w = w*Wn)
		T[i] = F[i] + G[i]*w , T[i+(ln>>1)] = F[i] - G[i]*w;
}
int main()
{
	scanf("%d%d",&n,&m);
	int x;
	for(int i = 0 ; i <= n ; ++i) scanf("%d",&x) , A[i].x=x;
	for(int i = 0 ; i <= m ; ++i) scanf("%d",&x) , B[i].x=x;
	lim = 1;
	while(lim <= n + m) lim <<= 1;
	FFT(lim , A , 1);
	FFT(lim , B , 1);
	for(int i = 0 ; i <= lim ; ++i) A[i] = A[i] * B[i];
	FFT(lim , A , -1);
	for(int i = 0 ; i <= n + m ; ++i)
		printf("%d ",(int)(A[i].x / lim + 0.5));
}

（sb luogu竟出锅，这个会输出0？？）

然后附上pks的迭代版参考代码（我明天肯定写.jpg

现在是我的了qwq

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
#include <cstdio>
#include <cstdlib>
#include <algorithm>
#include <iostream>
#include <cmath>
#define maxn 4000005
int n , m , lim , L , R[maxn];

const double pi = acos(-1.0);
struct Complex
{
	double x,y;
	Complex operator + (const Complex p)const{
		return (Complex){x+p.x,y+p.y};
	}
	Complex operator - (const Complex p)const{
		return (Complex){x - p.x , y - p.y};
	}
	Complex operator * (const Complex p)const{
		return (Complex){x*p.x-y*p.y , y*p.x+x*p.y};
	}
}A[maxn] , B[maxn];

void FFT(Complex* T , int op)
{
	for(int i = 0 ; i < lim ; ++i)
	   	if(i < R[i]) 
			std::swap(T[i] , T[R[i);
	for(int i = 1 ; i < lim ; i <<= 1) // length
	{
		Complex Wn = (Complex){(double)cos(pi / i) , (double)op * sin(pi / i)};
		for(int j = 0 ; j < lim ; j += (i << 1)) // beginning
		{
			Complex w = (Complex){1 , 0};
			for(int l = 0 ; l < i ; ++l , w = w * Wn)
			{
				Complex x = T[j + l] , y = w * T[j + i + l];
				T[j + l] = x + y , T[j + i + l] = x - y;
			}
		}
	}	

}
int main()
{
	scanf("%d%d",&n,&m);
	for(int i = 0 ; i <= n ; ++i) scanf("%lf",&A[i].x) ;
	for(int i = 0 ; i <= m ; ++i) scanf("%lf",&B[i].x) ;
	lim = 1;
	while(lim <= n + m) lim <<= 1 , ++L;
	for(int i = 0 ; i < lim ; ++i) 
		R[i] = (R[i >> 1] >> 1) | ((i & 1) << (L - 1));
	FFT(A , 1);
	FFT(B , 1);
	for(int i = 0 ; i <= lim ; ++i) A[i] = A[i] * B[i];
	FFT(A , -1);
	for(int i = 0 ; i <= n + m ; ++i)
		printf("%d ",(int)(A[i].x / lim + 0.5));
}

注意迭代版是$(cos(Pi / j), flag * sin(Pi / j))$，因为这里的$J$是中点。。。

迭代版虽然并没有什么难一点的原理，但我感觉如果不用要不了多久就忘了，画一画迭代树可以重新退出来？

多项式之NTT与任意模数NTT

preface

很大一部分学习自Flower_pks（看不懂的）

参考了成爷但又想再参考点别的

安利rvalue(实际上粘过来的时候我还没读)

读了，感觉极其良好。

原根

定义:

对于两个正数 $(a,m)=1$ , $\exists d$ $a^d ≡ 1 (\mod m)$

由此定义$a$对模$m$的指数$\delta m(a) $,为使$a^d ≡ 1$的最小的$d$.由上可知$d_{max} = \varphi(m)$.

我们把使得$\delta m(a) = \varphi(m)$的$a$称为是$m$的原根.

$G$是模数$P$的原根满足

$G^{p-1}\mod p = 1$
$\forall k , j \in [0,\varphi(p)) , G^{j} \neq G^{k} (k \neq j)$

为什么关于为什么在$[0,\delta(p))$下互不相同，大概可以反证一下：

首先可以肯定的是原根次幂在模意义下具有循环节（广义欧拉定理保证任意数都成立（但是不会证明)），我们设最小的使$G^{r} \equiv 1 \mod p$的$r$为$\delta(p)$ , 因为$G$是原根，所以$\delta(p) = \varphi(p)$ . 设$a ,b \in [0,\delta(p))$ , 如果$G^a \equiv G^b (\mod p~) , a < b$ , 则必有$G^{b-a} \equiv 1 \mod p$ ， 因此导致矛盾..

模数$P$有原根的等价条件是$P=2,4,p^n,2p^n.p \in prime \and p \neq 2$

但是我们在使用正常NTT的时候只会使用费马素数，也就是第三种$n=1 , p = a2^k + 1$

具体为什么可以看下面。如果没看懂就再看一遍

关于如何求原根,可能只能暴力枚举..一般记住$99244353$的原根是$3$

我们可以把$G^{k}$与$\omega_{n}^{k}$对比一下，前者在模意义下和后者都满足互不相同。

回顾FFT

我们思考一下FFT如何实现快速变换的。

  1. $\omega_{n}^{k} , k \in [0,n-1]$互不相同
  2. $\{(\omega{n}^{k})^2\} = \{(\omega{\frac{n}{2}}^{k})^2\}$ , 通过构造关于$x^2$的多项式即可进行分治计算，并且迅速求出另一半。
  3. $\sum{k=1}^{n-1}(\omega{n}^{j-i})^k = \begin{cases} 0 ~(i \neq j) \\ n ~(i = j) \\ \end{cases}$可以使用相同复杂度的算法进行IDFT

回顾到此完毕。

数论变换NTT

看Flower_pks的好像并没有看懂（符号貌似有些混乱），然后看了看challestand看懂了。

然后看了看发现也没有看懂 …

其实我会只是想copy一下，既然这样我还是自己写吧

设模数是$p = a2^k+1$

这个模数$p$必须保证$p-1$的约数个数大于你想要NTT的多项式长度。后面会说明。

发现我蠢了一下。

我们设$g_n = G^{\frac{p-1}{n}}$

这里肯定保证$n | (p-1)$

对于消去引理

$g_{dn}^{dk} = G^{\frac{dk(p-1)}{dn}} = G^{\frac{k(p-1)}{n}} = g_n^k$

证明完毕。

对于折半引理

首先我们发现$\frac{p-1}{n}=a$

所以我们先证明

$(n-1)a \leq p-2$

这样保证我们取的值均不相同。

把$a = \frac{p-1}{n}$带入即可。

接下来我们就可以证明折半引理了

我们应该证明

$g{n}^{k + \frac{n}{2}} \equiv -g{n}^{k}(\mod p~)$

这个就等价于

$g_{n}^{\frac n2} \equiv -1\mod p$

对$g_{n}^{n} \equiv 1 \mod p$开方困扰了我很久。

按理说普通模数应该是有好几个根的，但是这里我们模的是一个质数。

$(g{n}^{\frac n2})^2 \equiv 1 \mod p \Longleftrightarrow (g{n}^{\frac n2} + 1)(g_{n}^{\frac n2}-1) \equiv 0 \mod p$

$\Longrightarrow p ~| ~(g{n}^{\frac n2} + 1)(g{n}^{\frac n2}-1) \Longrightarrow g_{n}^{\frac n2} = \pm 1$

这样我们就完成了折半引理的证明。

到这里我们发现与单位根在复平面上均匀取点很相似，原根也在一个对称环上取值，

最后是我们为了保证可以用相同的方式进行逆运算还原，证明求和引理。

$\sum{i=0}^{n-1}(g{n}^{k})^j = \frac{g_{n}^{nk}-1}{g_n^k-1}$

同样当且仅当$k=n$上述等于$n$.

算法其他部分可以发现和FFT完全相同，包括构造两个多项式使得

$A(x) = A_0(x^2) + xA_1(x^2)$

这也是算法的核心部分。

最后我们来写一下NTT和INTT的式子，只需要把DFT和IDFT的单位根$\omega_n^k$根据上述性质替换成$g_n^k$即可

$DFT(gn^k)=\sum\limits{i=0}^{n-1}a_ig_n^{ik}$

$IDFT(yk) = \frac 1n\sum\limits{i=0}^{k}y_kg_n^{-ik}$

小结

重复一下

整个NTT原理我们一共证明了4条和FFT类似的性质：

  1. 对于消去引理

$g_{dn}^{dk} = G^{\frac{dk(p-1)}{dn}} = G^{\frac{k(p-1)}{n}} = g_n^k$

  1. 值的互不相同
    $\frac{p-1}{n}=a$
    $(n-1)a \leq p-2$

这样保证我们取的值均不相同。

把$a = \frac{p-1}{n}$带入即可使用放缩证明。

  1. 折半引理（用于分治过程）

$(g{n}^{\frac n2})^2 \equiv 1 \mod p \Longleftrightarrow (g{n}^{\frac n2} + 1)(g_{n}^{\frac n2}-1) \equiv 0 \mod p$

$\Longrightarrow p ~| ~(g{n}^{\frac n2} + 1)(g{n}^{\frac n2}-1) \Longrightarrow g_{n}^{\frac n2} = \pm 1$

  1. 求和引理（用于逆运算）

$\sum{i=0}^{n-1}(g{n}^{k})^j = \frac{g_{n}^{nk}-1}{g_n^k-1}$
同样当且仅当$k=n$上述等于$n$.其他情况下均为0
因为这条和FFT相同的性质，范德蒙特矩阵的证明在这里依然成立。

好像把前面内容都复制了一遍。

上述所有推导的除法均需要在模意义下进行，NTT算法保证精度。

突然懒得写，就找了个看上去不错的，反正就是一个替换。。

不存在的不到20分钟就写完了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
#include <cstdio>
#include <cstdlib>
#include <algorithm>
#include <iostream>
#define maxn 4000005
const int mod = 998244353 , G = 3 , Gi = 332748118;
int rev[maxn] , A[maxn] , B[maxn] , invN , n , m , lim;

inline int pow(int x , int y)
{
	int ans = 1 , base = x;
	for(  ; y ; y >>= 1 , base = 1ll * base * base % mod)
		if(y & 1)
			ans = 1ll * ans * base % mod;
	return ans;
}

inline void NTT(int* T , int op)
{
	for(int i = 1 ; i <= lim ; ++i)
		if(i < rev[i]) std::swap(T[i] , T[rev[i);
	for(int k = 1 ; k < lim ; k <<= 1)
	{
		int Gn = pow(op ? G : Gi , (mod - 1) / (k << 1));
		for(int j = 0 ; j < lim ; j += (k << 1))
		{
			int Gk = 1;
			for(int l = 0 ; l < k ; ++l , Gk = 1ll * Gk * Gn % mod)
			{
				int nx = T[j + l] , ny = 1ll * T[j + l + k] * Gk % mod;
				(T[j + l] = nx + ny) %= mod , (T[j + l + k] = nx - ny + mod) %= mod;
			}
		}
	}
}

int inv(int x){
	return x == 1 ? x : 1ll * (mod - mod / x) * inv(mod % x) % mod;
}
int main()
{
	scanf("%d%d",&n,&m);
	for(int i = 0 ; i <= n ; ++i) scanf("%d",&A[i]);
	for(int i = 0 ; i <= m ; ++i) scanf("%d",&B[i]);
	lim = 1;
	while(lim <= n + m) lim <<= 1;
	for(int i = 1 ; i <= lim ; ++i) rev[i] = (rev[i >> 1] >> 1) | ((i & 1) * (lim >> 1));
	NTT(A , 1) , NTT(B , 1);
	for(int i = 0 ; i <= lim ; ++i) A[i] = 1ll * A[i] * B[i] % mod;
	NTT(A , 0); invN = inv(lim);
	for(int i = 0 ; i <= n + m ; ++i) printf("%d ",1ll * A[i] * invN % mod);
}

多项式求逆

preface

大概是一个比较重要的算法了。

题目

给定多项式$F(x)$

求出$G(x)$使得$F(x)G(x) \equiv 1 \mod p$

$ p=998244353$

前置知识

倍增

都会。

NTT优化卷积乘法

都会

正式

多项式求逆，顾名思义就是求一个多项式的逆元。

求逆这个概念很广泛，任何有单位元的东西大都存在逆.

比如矩阵，模意义，或者群。

我们先看看多项式求逆的暴力算法。

假设$F(x) = \sum\limits{i=0}^{n-1}a_ix^i$ , $G(x)=\sum\limits{i=0}^{n-1}b_ix^i$

假设模$x^n$

我们有方程组！

$\begin{cases} a0b_0=1 \\ a_1b_0+a_0b_1=0\\ …\\ \sum\limits{i=0}^{n-1}aib{n-i} = 0\end{cases}$

如果暴力求解的话时间复杂度是$O(n^2)$

只需要从第一个开始解并不断代入即可。

1
2
3
4
5
6
b0 ← 1 / a0
for i ← 1 to m - 1
	bi ← 0
	for j ← 0 to i - 1
		bi ← bi - bj * ai - j
	bi ← bi / a0

可以得到一个结论：一个多项式有逆元当且仅当它的常数项存在逆元，且一个多项式的逆元是唯一的。

倍增+NTT优化

如何优化这个过程呢？

如果我们知道此时，我们可以抛开模意义去谈这件事情了。如果一个无穷级数是一个多项式的逆，则它的系数就被无穷多个方程组成的方程组约束。前面也看到过，如果模的是$x^k$，那它就会有$k$个方程去约束它。

我们能不能快速由$[b0….b{k-1}]$得到$[b0…b{2k-1}]$呢？（这里不是$b_{2k-2}$应该是实现上的原因吧。。）

推导后可以使用倍增。

假设当前模$x^k$ , 这个$k-1$项的多项式是$g_k(x)$

有$f(x)g_k(x) \equiv 1 \mod x^k$

显然$g_{2k}(x) \equiv g_k(x) \mod x^k$

$(g{2k}(x) - g{k}(x)) \equiv 0 \mod x^k$

因为是同余0，很容易发现模数和左边可以同时平方（其它情况应该并不可以）

$g{2k}^2(x) + g{k}^2(x)-2g_{2k}(x)g_k(x) \equiv 0 \mod x^{2k}$

此时我们同时乘上$f(x)$ , 根据定义$g_{2k}(x)f(x) \equiv 0 \mod x^{2k}$

$g{2k}(x) + g{k}^2(x)f(x) - 2g_{k}(x) \equiv 0 \mod x^{2k}$

移项可得

$g_{2k}(x) \equiv g_k(x)[2-g_k(x)f(x)] \mod x^{2k}$

上面的通过两次$O(nlogn)$多项式乘法即可完成。

总的时间复杂度

$T(n) = T(\frac n2)+O(nlogn)$

求一下和就是$T(n) = O(nlogn)$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
#include <cstdio>
#include <cstdlib>
#include <algorithm>
#include <iostream>
#define maxn 500005
const int mod = 998244353 , G = 3 , Gi = 332748118;

int f[maxn] , g[maxn] , t[maxn] , n , rev[maxn];

inline int pow(int x , int y)
{
	int ans = 1 , base = x;
	for( ; y ; y >>= 1 , base = 1ll * base * base % mod)
		if(y & 1)
			ans = 1ll * ans * base % mod;
	return ans;
}

inline void NTT(int* f , int lim , int op)
{
	for(int i = 0 ; i < lim ; ++i)
		rev[i] = (rev[i >> 1] >> 1) | (i & 1) * (lim >> 1);

	for(int i = 0 ; i < lim ; ++i)
		if(i < rev[i])	std::swap(f[i] , f[rev[i);
	for(int k = 1 ; k < lim ; k <<= 1)
	{
		int Gn = pow(op ? G : Gi , (mod - 1) / (k << 1));
		for(int j = 0 ; j < lim ; j += (k << 1))
		{
			int Gk = 1;
			for(int l = 0 ; l < k ; ++l , Gk = 1ll * Gk * Gn % mod)
			{
				int nx = f[j + l] , ny = 1ll * f[j + l + k] * Gk % mod;
				f[j + l] = (nx + ny) % mod , f[j + l + k] = (((nx - ny) % mod) + mod) % mod;
			}
		}
	}
}

int inv(int x){
	return x == 1 ? x : 1ll * (mod - mod / x) * inv(mod % x) % mod;
}

inline void InvPoly(int* f , int* g , int ln)
{
	g[0] = inv(f[0]);

	for(int i = 1 , j = 4 ; i < ln ; i <<= 1 , j <<= 1)
	{
		int iv = inv(j);
		for(int k = 0 ; k < (i << 1) ; ++k)
			t[k] = f[k];
		NTT(t , j , 1) , NTT(g , j , 1);
		for(int k = 0 ; k < j ; ++k)
			g[k] = (2 - 1ll * t[k] * g[k] % mod) * g[k] % mod;
		NTT(g , j , 0);

		for(int k = 0 ; k < j ; ++k) g[k] = 1ll * g[k] * iv % mod; // Important!!!!!
		
		for(int k = i << 1 ; k < j ; ++k)
			g[k] = 0;
		for(int k = 0 ; k < j ; ++k)
			t[k] = 0;
	}
}

int main()
{
	scanf("%d",&n);
	for(int i = 0 ; i < n ; ++i) scanf("%d",&f[i]);
	int x = 1 ; for( ; x < n ; x <<= 1);
	InvPoly(f , g , x);
	for(int i = 0 ; i < n ; ++i)
		printf("%d ",(g[i] + mod) % mod);

}

接下来我们推一推常用的分治FFT如何使用多项式求逆来解决

分治FFT

给定序列$g[1….n-1]$

设$f_0=1$

$fi = \sum{i=1}^{i}f_{i-j}g_j$

求出每个$f_i , i \in [1,n-1]$

题解

由于前面的项必须先算出来才能算后面的,所以不能直接FFT优化.

其实想到了基于计算时间的分治了,但是我居然没看出这个卷积形式该怎么用FFT……

原式在不考虑顺序的情况下就相当于$f_{i+j}=\sum f_ig_j$

在分治的时候我们会先递归左边然后考虑左边对右边的贡献.

注意一个事情，我就是因为这个才没写对….

对于递归完左边在当前区间算卷积对区间$f{[mid,r)}$应该是$f{[l,mid)} * g_{[1,r-l]}$ ， $f$和$g$的区间显然是不一样的……

所以分治中的卷积就是NTT了，算完之后只需要把右边那一部分$[mid,r)$加到答案里就可以了。

区间开闭还是不确定，所以必须写一写…..

时间复杂度$O(nlog^2n)$（听说多项式求逆可以做到$O(nlogn)$）

代码弃了，边界极其难调（上面的分析我很良心的写对了）而且被多项式求逆吊起来打。多项式求逆启动……

设$F(x) = \sum\limits_{i=0}^{n-1}a_ix^i$

$G(x) = \sum\limits_{i=0}^{n-1}b_ix^i$

$F$卷积$G$会平移一项，由于是无穷级数就变成了向前平移一项。

体会了一下这种通过生成函数转多项式求逆的方法的核心:利用题目给定的关系构造可以替换的多项式….至于怎么想出来就很难说了……

这两个多项式我们进行卷积，发现后面可以替换！

我们可以假定$g_0=0$，这并不会影响正确性。

$F(x)G(x) = \sum\limits{i=1}^{\infty}x^i\sum\limits{j=0}^{i-1}fjg{i-j}=\sum\limits{i=1}^{\infty}f{i+1}x^i = F(x) - f_0x^0$

剩下的就好办了。移项即可。

$F(x) = \frac{f_0}{1-G(x)} = (1-G(x))^{-1}$

然后我们只需要最高$n-1$次项的系数，所以在$\mod x^n$下求逆即可(不然也求不出来)

多项式求逆即可。

我去找了几本书看了下，发现似乎并没有很好的关于这方面的，好像数学女孩不错，强烈安利买一套（第三本离散数学太枯燥了点）。

感觉数学竞赛来了肯定爆切。

刚写完多项式求逆的我怎么会咕咕咕呢？
Code:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
#include <cstdio>
#include <cstdlib>
#include <algorithm>
#include <iostream>
#define maxn 500005
const int mod = 998244353 , G = 3 , Gi = 332748118;

int f[maxn] , g[maxn] , t[maxn] , n , rev[maxn];

inline int pow(int x , int y)
{
	int ans = 1 , base = x;
	for( ; y ; y >>= 1 , base = 1ll * base * base % mod)
		if(y & 1)
			ans = 1ll * ans * base % mod;
	return ans;
}

inline void NTT(int* f , int lim , int op)
{
	for(int i = 0 ; i < lim ; ++i)
		rev[i] = (rev[i >> 1] >> 1) | (i & 1) * (lim >> 1);

	for(int i = 0 ; i < lim ; ++i)
		if(i < rev[i])	std::swap(f[i] , f[rev[i);
	for(int k = 1 ; k < lim ; k <<= 1)
	{
		int Gn = pow(op ? G : Gi , (mod - 1) / (k << 1));
		for(int j = 0 ; j < lim ; j += (k << 1))
		{
			int Gk = 1;
			for(int l = 0 ; l < k ; ++l , Gk = 1ll * Gk * Gn % mod)
			{
				int nx = f[j + l] , ny = 1ll * f[j + l + k] * Gk % mod;
				f[j + l] = (nx + ny) % mod , f[j + l + k] = (((nx - ny) % mod) + mod) % mod;
			}
		}
	}
}

int inv(int x){
	return x == 1 ? x : 1ll * (mod - mod / x) * inv(mod % x) % mod;
}

inline void InvPoly(int* f , int* g , int ln)
{
	g[0] = inv(f[0]);

	for(int i = 1 , j = 4 ; i < ln ; i <<= 1 , j <<= 1)
	{
		int iv = inv(j);
		for(int k = 0 ; k < (i << 1) ; ++k)
			t[k] = f[k];
		NTT(t , j , 1) , NTT(g , j , 1);
		for(int k = 0 ; k < j ; ++k)
			g[k] = (2 - 1ll * t[k] * g[k] % mod) * g[k] % mod;
		NTT(g , j , 0);

		for(int k = 0 ; k < j ; ++k) g[k] = 1ll * g[k] * iv % mod; // Important!!!!!
		
		for(int k = i << 1 ; k < j ; ++k)
			g[k] = 0;
		for(int k = 0 ; k < j ; ++k)
			t[k] = 0;
	}
}

int main()
{
	scanf("%d",&n);
	for(int i = 1 ; i < n ; ++i) scanf("%d",&f[i]) , f[i] = -f[i];
	f[0] = 1;
	int x = 1 ; for( ; x < n ; x <<= 1);
	InvPoly(f , g , x);
	for(int i = 0 ; i < n ; ++i)
		printf("%d ",(g[i] + mod) % mod);

}

接下来的内容都比较有难度了！

Taylor展开

泰勒多项式展开的项数越多，曲线拟合的越好。

在数学中，泰勒公式是一个用函数在某点的信息描述其附近取值的公式。这个公式来自于微积分的泰勒定理，泰勒定理描述了一个可微函数，如果函数足够光滑的话，在已知函数在某一点的各阶导数值的情况之下，泰勒公式可以用这些导数值做系数构建一个多项式来近似函数在这一点的邻域中的值，这个多项式称为泰勒多项式。泰勒公式还给出了余项即这个多项式和实际的函数值之间的偏差。泰勒公式得名于英国数学家布鲁克·泰勒。他在1712年的一封信里首次叙述了这个公式，尽管1671年詹姆斯·格雷高里已经发现了它的特例。 拉格朗日在1797年之前，最先提出了带有余项的现在形式的泰勒定理。

泰勒公式

泰勒公式的初衷是用多项式来近似表示函数在某点周围的情况。比如说，指数函数$e^x$在$x = 0$的附近可以用以下多项式来近似地表示：
:$ \textrm{e}^x \approx 1 + x + \frac{x^2}{2!} + \frac{x^3}{3!} + \cdots + \frac{x^n }{n!}.$

称为指数函数在0处的$n$阶泰勒展开公式。这个公式只对$0$附近的$x$有用，$x$离$0$越远，这个公式就越不准确。实际函数值和多项式的偏差称为泰勒公式的余项。
:$R_n(x) = \textrm{e}^x - \left(1 + x + \frac{x^2}{2!} + \frac{x^3}{3!} + \cdots + \frac{x^n}{n!}\right).$

泰勒定理

对于一般的函数，泰勒公式的系数的选择依赖于函数在一点的各阶导数值。这个想法的原由可以由微分的定义开始。微分是函数在一点附近的最佳线性近似：
: $f(a + h) = f(a) + f^{\prime}(a)h + o(h)$，其中$o(h)$ 是比h 高阶的无穷小。
也就是说$f(a + h) \approx f(a) + f^{\prime}(a)h $，或$f(x) \approx f(a) + f ^{\prime}(a)(x - a) $。

注意到$f(x)$ 和$f(a)+f^{\prime}(a)(x - a)$ 在a 处的零阶导数和一阶导数都相同。对足够光滑的函数，如果一个多项式在a 处的前n 次导数值都与函数在a 处的前n 次导数值重合，那么这个多项式应该能很好地近似描述函数在a 附近的情况。以下定理说明这是正确的：

设 n 是一个正整数。如果定义在一个包含a 的区间上的函数f 在a 点处n+1 次可导，那么对于这个区间上的任意x，都有：
$ f(x) = f(a) + \frac{f(a)}{1!}(x - a) + \frac{f^ {(2)}(a)}{2!}(x - a)^2 + \cdots + \frac{f^{(n)}(a)}{n!}(x - a)^n + R_n(x). $

其中的多项式称为函数在a 处的泰勒展开式，剩余的$R_n(x)$ 是泰勒公式的余项，是$(x - a)^n$ 的高阶无穷小。

$R_n(x)$ 的表达形式有若干种，分别以不同的数学家命名。

带有皮亚诺型余项的泰勒公式说明了多项式和函数的接近程度：
$ f(x) = f(a) + \frac{f(a)}{1!}(x - a) + \frac{f^ {(2)}(a)}{2!}(x - a)^2 + \cdots + \frac{f^{(n)}(a)}{n!}(x - a)^n + o[(x - a)^{n}] $
也就是说，当x 无限趋近$a$ 时，余项$R_n(x)$ 将会是$(x - a)^{n}$ 的高阶无穷小，或者说多项式和函数的误差将远小于$(x - a)^{n}$。这个结论可以由下面更强的结论推出。

带有拉格朗日型余项的泰勒公式可以视为拉格朗日微分中值定理的推广：
$ f(x) = f(a) + \frac{f(a)}{1!}(x - a) + \frac{f^ {(2)}(a)}{2!}(x - a)^2 + \cdots + \frac{f^{(n)}(a)}{n!}(x - a)^n + \frac{ f^{(n+1)}(\theta) }{(n + 1)!}(x - a)^{(n+1)} $

即$R_n(x) = \frac{ f^{(n+1)}(\theta) }{(n + 1)!}(x - a)^{(n+1)}$，其中$\theta \in (a, x)$

带有积分型余项的泰勒公式可以看做微积分基本定理的推广
$ R_n(x) = \int_a^x \frac{f^{(n+1)} (t)}{n!} (x - t)^n \, dt,$

余项估计

拉格朗日型余项或积分型余项可以帮助估计泰勒展开式和函数在一定区间之内的误差。设函数在区间$[a-r,a+r]$ 上$n$ 次连续可微并且在区间$(a-r,a+r)$ 上$n+1$ 次可导。如果存在正实数$M_n$ 使得区间$(a-r,a+r)$里的任意$x$都有$|f^{(n+1)}(x)| \le M_n$，那么：

$ f(x) = f(a) + \frac{f(a)}{1!}(x - a) + \frac{f^ {(2)}(a)}{2!}(x - a)^2 + \cdots + \frac{f^{(n)}(a)}{n!}(x - a)^n + R_n(x),$

其中$|R_n(x)| \le M_n \frac{r^{n+1}}{(n+1)!}$。这个上界估计对区间$(a-r,a+r)$里的任意$x$ 都成立，是一个一致估计。

如果当$n$趋向于无穷大时，还有$M_n \frac{r^{n+1}}{(n+1)!} \rightarrow 0$，那么可以推出$R_n(x) \rightarrow 0$，$f$ 是区间$(a-r,a+r)$上解析函数（局部上的幂级数近似）。$f$ 在区间$(a-r,a+r)$ 上任一点的值都等于在这一点的泰勒展开式的极限。

多元泰勒公式

对于多元函数，也有类似的泰勒公式。设$B(a, r )$是欧几里得空间$R^N$中的开集|开球，$ƒ $是定义在$B(a, r ) $的闭包上的实值函数，并在每一点都存在所有的$n+1 $次偏导数。这时的泰勒公式为：
:对所有$x\in \mathbf{B}(a, r)$，
:$f(x)=\sum{|\alpha|=0}^n\frac{1}{\alpha!}\frac{\partial^\alpha f(a)}{\partial x^\ alpha}(xa)^\alpha+\sum{|\alpha|=n+1}R_{\alpha}(x)(xa)^\alpha$

:其中的$ \alpha $ 是多重指标，即$ |\alpha |=\alpha _1+\alpha _2+…+\alpha _n $ , $ \alpha !=\alpha _1!\cdot\alpha _2!\cdot…\cdot\alpha _n! $ 。
:若$ x=(x_1,x_2,…,x_n) $ ,则记
:$ x^{\alpha }=x_1^{\alpha _1}x_2^{\alpha _2}…x_n^{\alpha _n} $.
:$ \frac{\partial^\alpha f(a)}{\partial x^\alpha}=\frac{\partial ^{\alpha _1+\alpha _2+…+\alpha _n}f(a )}{\partial x_1^{\alpha _1}x_2^{\alpha _2}…x_n^{\alpha _n}} $.

其中的余项也满足不等式：
:对所有满足$\alpha = n+1 $的α，$|R{\alpha}(x)|\le\sup{y\in\bar{B} }\left|\frac{1}{\alpha!}\frac{\partial^\alpha f(y)}{\partial x^\alpha}\right|$

特别地，多元形式的泰勒公式可表示为：
:$ f(a +h)=\sum{k=0}^{m}\sum{|\alpha |=k}\frac{\partial^\alpha f(a)}{\partial x^ \alpha}h^{\alpha }+Rm $
:其中$ R_m=\sum{|\alpha |=m+1}\frac{\partial ^{\alpha }f(a +\theta h)}{\alpha !}h^{\alpha }$
在应用上述公式时，特别重要的是展开式的前三项，即：
:$ f(a +h)=f(a )+\frac{\partial f}{\partial x1}(a )h_1+…+\frac{\partial f}{\partial x_n}(a )h_n+\frac{1}{2}\sum{i,j=1}^{n}\frac{\partial ^{2}f}{\partial x_i\partial x_j}(a )+…$
:运用雅可比矩阵与海森矩阵，则上式可表示为：
:$ f(a +h)=f(a )+Jf(a )h+\frac{1}{2}(h_1,…h_n)Hf(a )
\begin{pmatrix}
h_1\\
…\\
h_n\\
\end{pmatrix}+… $
:其中$ Jf(a ) $ 为雅可比矩阵，$ Hf(a) $ 为海森矩阵.

多项式除法

给定$n$次多项式$F(x)$和$m$次多项式$G(x)$.求一个$n-m$次多项式$Q(x)$和一个小于$m$次的多项式$R(x)$
使得

$F(x) \equiv G(x)Q(x) + R(x) \mod 998244353$

这个问题的构造还是很巧妙的。

设$A_R(x) = x^nA(\frac 1x)$

发现系数正好倒过来。。。

$F(\frac 1x) = G(\frac 1x)Q(\frac 1x) + R(\frac 1x)$
$x^nF(\frac 1x) = x^{n-m}Q(\frac 1x)x^mG(x) + x^{n-m+1}x^{m-1}R(\frac 1x)$
$F_R(x) = Q_R(x)G_R(x)+x^{n-m+1}R_R(x)$

这时如果我们模一下$x^{n-m+1}$

$Q_R(x) = F_R(x)G_R^{-1}(x) \mod x^{n-m+1}$

多项式求逆即可。

求出$Q$后只需要一个减法就可以求出$R$。
最后时间复杂度是$O(nlogn)$

代码咕一会。

http://vfleaking.blog.uoj.ac/slide/87#/

看这个好东西复习一波容斥和莫比乌斯反演。